Shrinking Constraints
The concept of shrinking constraints can be important for understanding some optimization solution analysis information provided by RiverWare and for understanding how the solution behaves in terms of adding new constraints to the optimization problem.
In water resource management policies, it is common to have constraints at different priorities that have the same form (same left-hand-side) and differ only in the right-hand-side constraint value. For example, assume that a reservoir Storage variable has a formal upper bound of 10,000 acre-ft. In the policy constraints, there is a high priority Maximum Storage constraint to not exceed 9,000 acre-ft. At a lower priority there is a Target Operating Range constraint that applies a more restrictive max Storage of 8,000 acre-ft. Typically it is desirable to be below this elevation, but it might not always be possible due to high inflows. Then at a lower priority there is a Target Operating Storage Point constraint that constrains the Storage equal to 7,000 acre-ft, if possible.
Note: Internally, all “equal-to” constraints are converted to an equivalent pair of constraints.
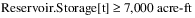
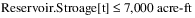
Together, in addition to the upper bound, there would be three constraints with the same left-hand-side (LHS), in order from highest priority (1) to lowest (3):
• Priority 1: 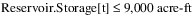
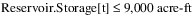
• Priority 2: 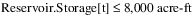
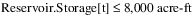
• Priority 3: 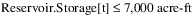
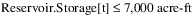
Note: In practice, there would typically be constraints on other variables at intervening priorities between the constraints with the same LHS. For simplicity here were are only looking at the constraints with common LHS.
Rather than add a new constraint to the optimization problem each time, RiverWare minimizes the size of the optimization problem by shrinking the lower priority constraints into the higher priority constraint of the same form.
The priority 1 constraint, when written as a soft constraint with a satisfaction variable would have the following form:
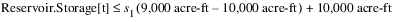
Assuming that the priority 1 constraint is fully satisfied, the priority 2 constraint would conceptually have the following form:
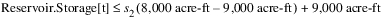
However, instead of adding a new constraint, RiverWare notices that the new constraint has the same LHS and only differs in the right-hand-side value, so it shrinks the priority 2 constraint into the priority 1 constraint in the following form.
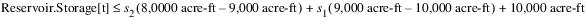
The less-than-or-equal-to portion of the priority 3 constraint would then shrink into this constraint in the same manner.
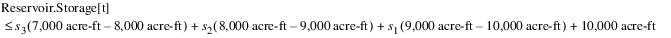
Note: All evaluation is done internally in RiverWare Optimization units, which are typically scaled SI units, not in user display units as shown here.
More generally, constraints with shrinking have the following form:
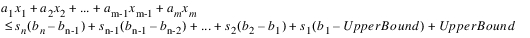
where each xm is a variable in the LHS of each of the constraints in the shrinking sequence, each am is the corresponding coefficient on the variable, each sn is the satisfaction variable associated with the constraint at the nth priority that contains a constraint with this common LHS, and each bn is the right-hand-side constraint value at the nth priority that contains a constraint with this LHS. UpperBound is the formal upper bound on the LHS. It is calculated by evaluating the LHS with each variable with a positive coefficient replaced by the variable’s upper bound and each variable with a negative coefficient replaced by the variable’s lower bound. For variables that correspond directly to a slot, the variable bounds are taken directly from the Upper and Lower Bounds set in the slot configuration. See Variable Bounds for details.
The form is the same for a “greater-than-or-equal-to constraint”, except that the LowerBound is used. The LowerBound is calculated by evaluating the LHS with each variable with a positive coefficient replaced by the variable’s lower bound and each variable with a negative coefficient replaced by the variable’s upper bound.
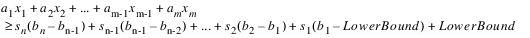
In the example above, if the priority 2 constraint were not fully satisfied, then that constraint would be frozen. (See Freezing Constraints for details about freezing constraints.) In that case, the priority 3 constraint (or any subsequent constraints with the same LHS) would never get added to problem. Because the LHS value was already locked in at priority 2, no lower priority constraints can change its value. Thus, there is no need to add any new constraints with the same LHS to the problem. In other words, RiverWare identifies if a new constraint would shrink to a constraint that is already frozen. If that is the case, then the new constraint does not get added to the problem. This can be important to understand when analyzing the solution. No solution analysis information will be provided for a constraint that would shrink to a constraint that was already frozen because the new constraint never gets added to the problem. If all of the constraints at one priority would shrink to constraints that are already frozen, then no new constraints get added to the problem at that priority, and thus there is no need to solve the problem at that priority. As a result, that priority will not show up in the standard diagnostic output with an objective value (percent satisfaction), nor will that goal appear in the Optimization Solution Analysis Tool. See Priority-oriented Optimization Solution Analysis Tool for details.
If some constraints from a given priority would shrink to frozen constraints, but others do not (i.e. there is still a solution at that priority, but some constraints introduced at that priority are omitted because they would not change the solution), the reporting of the satisfaction for the soft constraint derived objective depends on the type of derived objective that is selected. If the derived objective is Single Maximin or Repeated Maximin, then the satisfaction only reflects the satisfaction of the constraints that were formally added to the problem. It does not reflect the satisfaction of the constraints that were omitted (and would possibly have been violated). A tilde (~) is added to the reported satisfaction value to indicate that it is greater than the actual satisfaction from the user’s perspective because it does not include the omitted constraints. For a Summation derived objective, the reported average satisfaction is calculated as if the omitted constraints had been added to the problem. Thus it reflects the satisfaction from the user’s perspective, and no special notation is required.
If a frozen constraint shrinks to a higher priority constraint, the Optimization Solution Analysis Tool lists which constraint it shrinks to as part of the frozen constraint information (see Priority-oriented Optimization Solution Analysis Tool). Also, if a constraint is frozen, the solution analysis tool will report that all of its shrink to constraints were frozen as well. Without understanding how constraints shrink to earlier constraints, this can be confusing because it appears that a higher priority constraint was frozen even though the solution was not at the limit set by the constraint. Really it is the lowest priority constraint that shrank to that higher priority constraint that was forced to its limit and was frozen.
Revised: 01/05/2024