Economic Valuation User Methods
These methods model the economic valuation of hydropower during an optimization run using the Optimization controller. The category doesn’t exist in the Simulation and Rulebased Simulation controllers. The values are based either explicitly or implicitly on the replacement of thermal power sources and the associated cost savings. (The descriptions of possible optimization policy in this section are not intended to exactly show the syntax of the policy statements. This is in part because the policy syntax differs under the old Optimization controller and the new Optimization controllers.)
The methods in this category exactly parallel the methods in the Thermal Replacement Value category for simulation, with the exception that no attempt is made to attribute value to particular energy sources. Thus, simulation methods that are identical except for the order of evaluation map to a single optimization method. This optimization method is dependent on one of the appropriate simulation methods being selected.
All of the methods use the slot Avoided Operating Cost to represent the explicit or implicit savings to the thermal system from hydropower generation. The methods differ in how they compute Avoided Operating Cost. It is assumed that the user will write an objective function that either directly or indirectly maximizes Avoided Operating Cost.
In this description, anywhere it says Net Avoided Cost or Avoided Operating Cost, it should have either Thermal, Block, or Linear added to the beginning; that is, Linear Net Avoided Cost, depending on method selections.
Following are possible objectives:
Objective 1:
Maximize Net Avoided Cost
Maximize Net Avoided Cost
Net Avoided Cost is defined as the Avoided Operating Cost minus the value of energy used for generation and energy lost to spill:
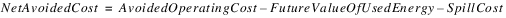
Future Value of Used Energy and Spill Cost are multislots that are assumed to be linked to the individual values on power reservoirs. The individual reservoir calculations use a power coefficient and a dollar value to translate releases into these costs.
An alternative to penalizing the Future Value of Used Energy and Spill Cost is to maximize the Total Cumulative Storage Value, a multislot with the expected value of all water remaining in storage. This multislot is expected to be linked to the Cumulative Storage Value on the individual reservoirs, where it is a piecewise linear function of storage.
Objective 2:
Maximize Avoided Operating Cost + Total Cumulative Storage Value (Final timestep)
Maximize Avoided Operating Cost + Total Cumulative Storage Value (Final timestep)
Optionally, the objective can subtract the following term, Total Cumulative Storage Value (Initial timestep).
Objective 3:
Maximize Avoided Operating Cost + Total Cumulative Storage Value (Final timestep) – Total Cumulative Storage Value (Initial timestep)
Maximize Avoided Operating Cost + Total Cumulative Storage Value (Final timestep) – Total Cumulative Storage Value (Initial timestep)
Subtracting this constant term does not effect the optimal solution, but the reported objective function value will now reflect the change in total Cumulative Storage Value, typically a more meaningful number.
In some cases a utility may be allocating additional energy from outside the basin. If data is specified for the slots described below, the optimization will automatically create variables for each column of the Allocated Detail Energy Slot. These variables are constrained to minimum and maximum values:
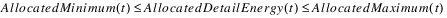
The Allocated Detail Energy is further constrained to meet periodic totals where the period is a multiple of the timesteps of the run. For example, a model with a 6 Hour timestep, might have a total daily energy target. More generally, the period is specified by the timesteps with non-zero values for Allocated Total Energy. The Allocated Detail Energy is required to meet the totals. For a daily period the constraint is:
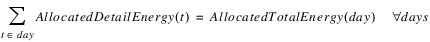
The user can further constrain allocated energy by selecting the Preferred Customer method from the Preferred Customer category.
Revised: 12/06/2024