Linearization, Approximation, and Replacement
Some slots, such as Storage and Outflow, correspond directly to decision variables in the Optimization problem. Other slots, such as Power, are translated into linear combinations of other decision variables. RiverWare automatically selects which substitution methods to use based on the slots referenced and the context in which they are referenced in the policy (goal). All substitution is done automatically behind the scenes in RiverWare. For all substitution methods, if the resulting expression is not a function of only decision variables, substitution continues using whatever method is appropriate until only decision variables remain.
Details of the substitution methods are given below.
Link Substitution
Link substitution replaces a linearized slot with the slots that it is linked to. An example is the substitution of a reach Inflow that can be a combination of Outflows from one or more other objects.
Constraint Substitution
Constraint substitution replaces expressions containing one linearized slot by equivalent expressions containing only one decision variable slot. For example, Pool Elevation is a linearized slot that has a direct relationship to Storage, a decision variable slot, defined by the Elevation Volume Table. A constraint such as Pool Elevation greater than or equal to some value can be replaced by an equivalent constraint on Storage.
Direct substitution will not work for constraints with multiple terms. For example, Operating Head cannot be replaced by a constant directly because Operating Head is Pool Elevation minus Tailwater Elevation, and thus there are two linearized slots on the left hand side of the constraint. When it is available, direct substitution is the preferred method for linearization because the only linearization error is the error in the table.
Expression Substitution
Expression substitution replaces a linearized slot with a linear expression of other slots. An example for Precipitation Volume is shown below.
In the above expression, Surface Area is itself a linearized variable that is a function of Storage. So Surface Area will be substituted by an expression in terms of Storage.
Variable Substitution
Variable substitution replaces a linearized slot with a known linear expression of other slots. Variable substitution can use direct substitution, a two dimensional linearization (tangent, two-point line or piecewise) or three-dimensional linearization (constant and multiple approximation). These methods are described below. RiverWare automatically chooses the correct linearization method to use based on the slot and the context of the policy expression.
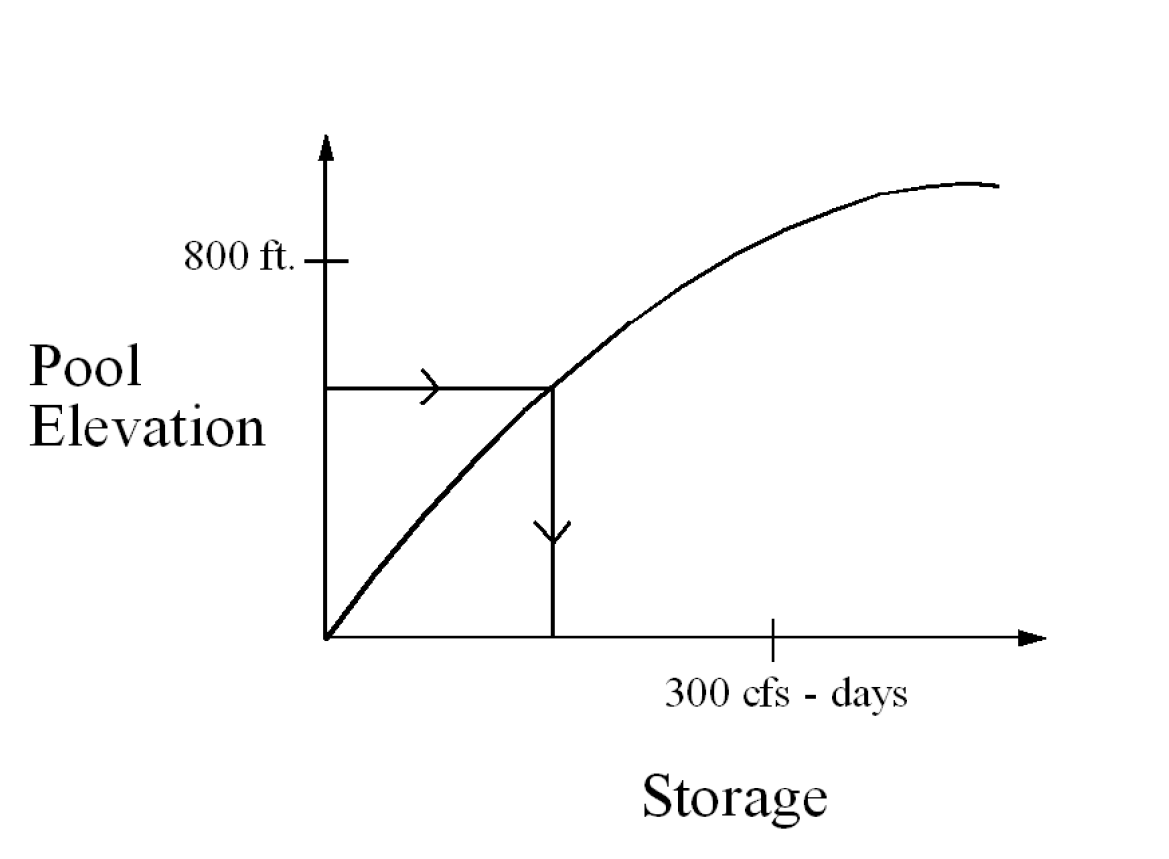
The mathematical functions used by RiverWare to model the relationships between two slots can be classified as convex, concave or nonconvex, nonconcave. Which linearization methods can be used to approximate a functional relationship between two slots and the accuracy of the approximation depends on the convexity of the function. Riverware expects a specific convexity for each functional relationship. If a user input function defined by a table slot does not match the expected convexity, an error is returned. An example of a concave function is the relationship between Pool Elevation and Storage. See Figure 4.16.
Figure 4.16
A convex function is the relationship between Unregulated Spill and Pool Elevation. See Figure 4.17.
Figure 4.17
A nonconvex, nonconcave function is the relationship between Canal Flow and Delta Elevation. See Figure 4.18.
Figure 4.18
A tangent approximation will over-approximate a concave function and under-approximate a convex function. A two-point (secant) approximation will under-approximate a concave function and over-estimate a convex function.
The points used to define the tangent, two-point line and piecewise approximations are specified in linearization parameter tables. These are slots with LP Param in the name. See Optimization Objects and Methods for details about LP Param table slots within individual slot and method descriptions.
Direct Substitution
Substitution replaces the a variable with the value of another variable from the linearization function table. For example, Pool Elevation is replaced by the equivalent Storage (see Figure 4.19). Values that are not listed directly in the table are approximated by linear interpolation. Substitution is only allowed for single term constraints. Substitution is generally the preferred linearization method when it is available because it has the least approximation error. RiverWare automatically uses this approach whenever there is a constraint with a single term.
Figure 4.19
Tangent Approximation
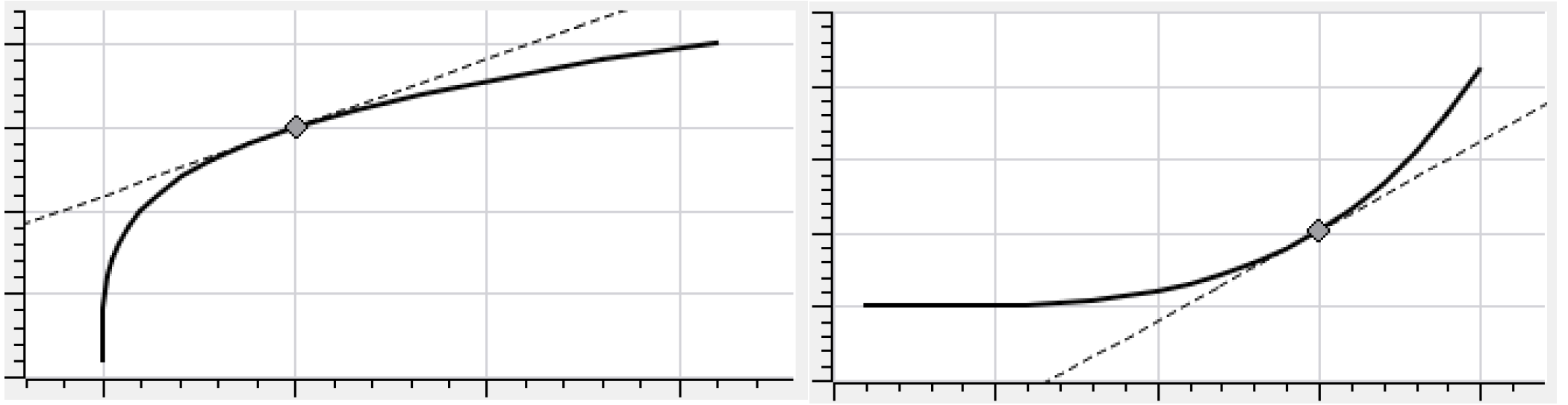
For the tangent approximation a nonlinear function is approximated as the line tangent to the function at a specified point. The same approximation point is used for every time step. Tangent is preferred when an over estimation is acceptable for a concave function or an under approximation is acceptable for a convex function. Tangent approximations are good when the value of a function will not vary greatly from the initial value (approximation point). Tangent approximations are not always available because of the errors they can introduce for certain types of functions. For example, tangent approximations are not used for Spill Capacities because it could result in a non-zero value for a function with a zero input. The best approximation point for a tangent to be taken at is the median value expected during the run.
Figure 4.20 Tangent approximations of a nonlinear function
Two-point Line Approximation
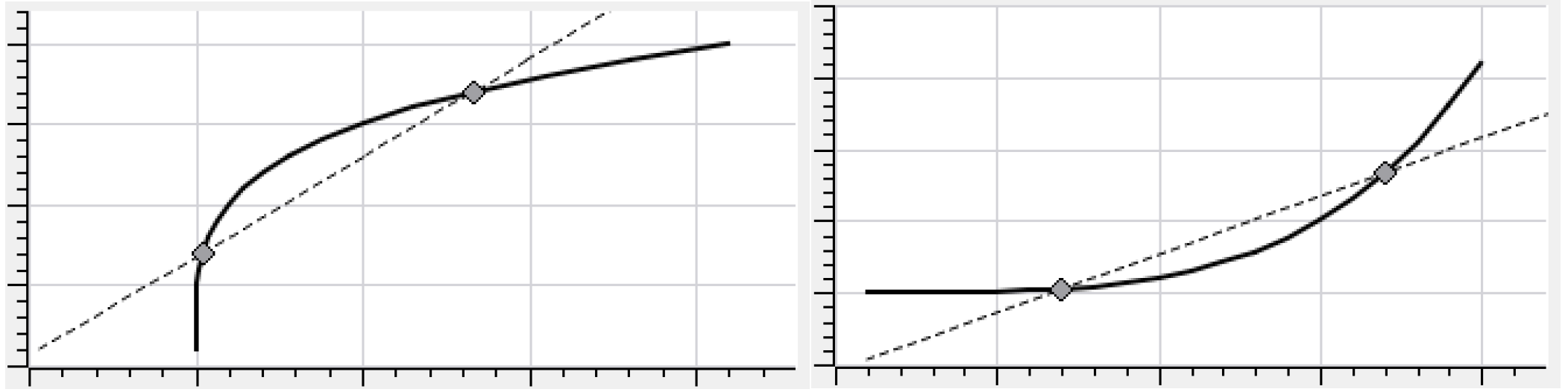
For the two-point line (secant) approximation a nonlinear function is approximated by a line through two points on the function. The two points are fixed and remain the same for every time step. Unlike the tangent approximation, the two point line approximation sometimes underestimates a function and sometimes overestimates a function. The best approximation points for a line are points that will define a line close to the expected values during the run.
Figure 4.21 Two-point line (secant) approximation
Piecewise Approximation
For a piecewise approximation a nonlinear function is approximated as a piecewise linear function. The x values for an arbitrary number of points are input into the third column of the LP Param table. Lines are generated between adjacent points. Several constraints are added to the LP model that make sure that the approximation will work.
As an example, Power (P) is a function of Turbine Release (Q). A piecewise approximation would be
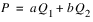
with the constraints
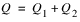
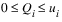
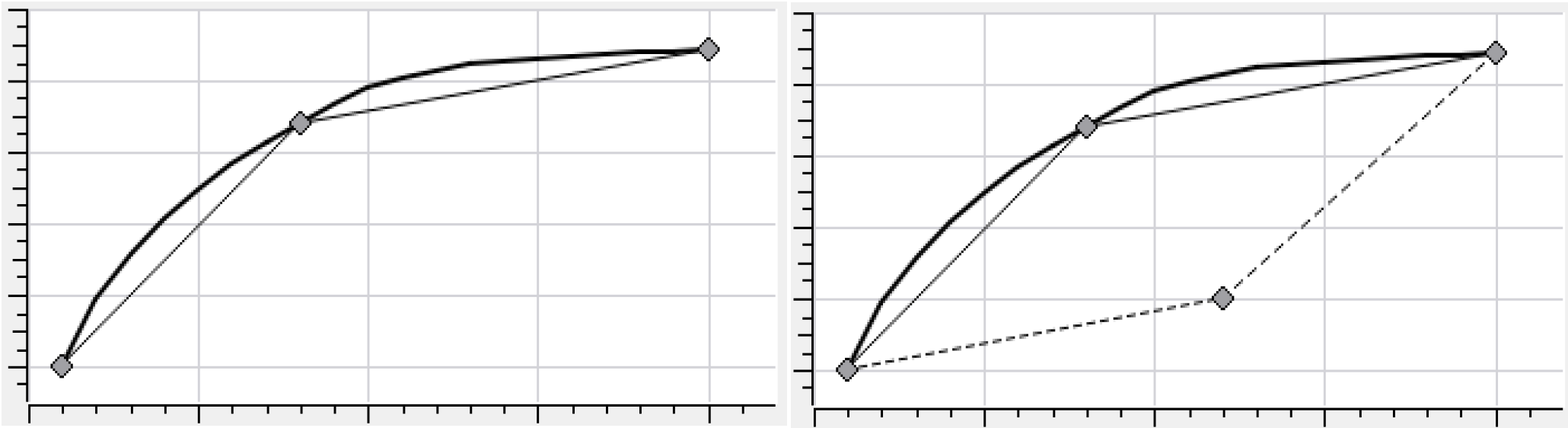
Where a and b are the slopes of the approximation lines and ui is the length of segment i. The optimization process can cheat when dealing with less than or equal constraints on concave functions and greater than or equal to constraints on convex functions. The figure below shows a piecewise approximation of a concave function using two lines (three points). If a minimization is done to this function or it is used with a less than or equal to constraint, the solution would try to pick values that correspond to the dashed line rather than the solid line. That is, it would use the pieces out of order. RiverWare prevents this use of pieces out of order by automatically using the two-line approximation in these cases. If substitution is not available, piecewise approximations are the next preferred linearization method because they can fit the curve closely and minimize the approximation error better than line or tangent generally can. With piecewise approximations it is best to cover the range of values of the function, especially in range of the expected values. Additional points should be included where there are breaks in the curve. A minimum of two points are required. As many points as desired may be used to fit the curve, but a larger number of points will increase the size of the optimization problem and could impact performance (run time).
Figure 4.22 Piecewise approximation of a concave function
Lambda Method
Note: This section is under development.
Revised: 12/06/2024