USACE‑SWD Modeling Techniques
Computing Reservoir Yield
This section provides instructions to convert an existing working USACE‑SWD model into a yield study using iterative MRM. A yield study is used to determine the largest average diversion that can be made from a single reservoir such that the reservoir will not drop below the bottom of conservation pool at any time during the run period. Other operating policies like Surcharge, Regulation Discharge, Flood Control, Low-flow Release, and Hydropower can be included in this analysis. The following files are needed for this analysis.
Note: These files were updated for RiverWare 7.3.
Contact riverware‑support@colorado.edu for the files that correspond to this document.
Contact riverware‑support@colorado.edu for the files that correspond to this document.
• YieldStudy.rls.gz. An MRM ruleset that controls the run iteration and determines the yield for each run.
• YieldStudy.obj. An importable data object containing the slots referenced by YieldStudy.rls.gz
• YieldStudy.sct. An optional SCT used to view the integer indexed slots in the data object imported from YieldStudy.obj
Figure 5.1 Yield study data object
Steps
Given a working model for a basin, to conduct a reservoir yield study, the following changes need to be made.
1. Import the yield study data object.
– Select the workspace menu item Workspace, then Objects, then Import Objects and import the file YieldStudy.obj.This will create a new data object named Yield Study Data.
The slots on this object used for input data are as follows.
– Reservoir Data for Bisection. The name of the reservoirs which are participating in the yield study should appear as the row labels of the Reservoir Data for Bisection Table Slot. Append rows as necessary using the Edit menu. Edit the row label as appropriate using the View, then Edit Row Labels menu. When editing row Labels, there is a useful button in the Edit Row Labels dialog to Set Label(s) to an Object Name. The yield study ruleset requires a lower limit on the yield for each individual reservoir. By default the algorithm will use 0.0cfs as the lower limit. If this is not a reasonable lower limit, you can provide an alternative value in the Minimum Yield column of the table. The yield study ruleset also requires an upper limit on the yield for each individual reservoir. By default it will use the average inflow, over the run, for each reservoir. If this is not a reasonable upper limit, you can provide an alternative value in the Maximum Yield column of the table. For certain algorithms, an Initial Yield to Try can be provided as a column.
– Convergence From Above, Convergence From Below. The scalar values representing how accurate the yield value should be above or below the exact answer: Convergence From Above and Convergence From Below.
– Yield Distribution. This optional periodic slot is used to specify factors for distributing the average yield throughout the year. The values in the slot are the fraction or percentage of the average yield to be applied to each timestep in the run. The values in this slot should average to 1.0 over the course of a year. A prerun rule will check that they average to 1.0 and stop the run if they do not. If this slot is to be used, makes sure to use the MRM rule Use Distribution Pattern. See Step 4., below.
• The remaining slots on this data object contain output values from the yield study. Most of them are indexed by the MRM run number.
– Yield. Integer indexed series slot contains the results of the analysis (indexed by the MRM run number). Append columns as necessary using the Edit menu. On the Yield slot, modify the column label (using the View, then Edit Column Labels menu) to match the reservoir's name. When editing column Labels, there is a useful button in the Edit Column Labels dialog to Set Label(s) to an Object Name.
– Reservoir Index. Integer indexed series slot that tracks which reservoir is being analyzed (indexed by the MRM run number). In a single reservoir study, this value will always be output as zero.
– Yield Upper Bound, Yield Lower Bound. Integer indexed series slots indicating the bounds used for the current iteration by the bisection method on the current reservoir (indexed by the MRM run number).
– Minimum Level Difference. Integer indexed series slot showing the minimum difference between pool elevation and the bottom of the conservation pool for the current reservoir at the current run (indexed by the MRM run number).
– Minimum Level Difference Date. Integer indexed series slot containing the date at which the Minimum Difference occurs.
– Critical Period Start Date, Critical Period End Date, and Critical Period Duration. These integer indexed slots have a unit type of DateTime. They are used to store the dates when the critical period starts, ends, and the duration, respectively.
– Estimated Yield Error. Integer Indexed series slot containing the underestimation error associated with the yield. This is calculated as the additional volume of water that must be released during the critical period, including an estimate of reduced evaporation, to lower the pool to the bottom of conservation pool on the critical date. See “Algorithms” for details on this calculation.
– Distribute Yield. Integer Indexed Series slot that keeps track of whether the user has configure to use a distribution pattern (value = 1) or a constant pattern (value = 0).
– Algorithm To Use. Integer Indexed Series slot that keeps track of whether the user has configure to use Bisection (value = 1), Heuristic A (value = 2) or Heuristic B (value = 3).
2. Disable diversions. For the purposes of the yield study, diversion is controlled by directly setting the reservoir Diversion slot values, so you will need to disable the Diversion and Water Users objects that would divert water from reservoirs participating in the yield study. This can be done in the Run Analysis dialog by selecting the object’s row and then selecting Object, then Disable Dispatching. This should only be done for the specific reservoirs for which you are finding the yield. The other reservoir’s Diversion and Water User objects could remain enabled as desired.
3. Load the standard rulebased simulation ruleset that represents the policy in the basin. Use the Workspace, then Policy menu. Disable aspects of the policy (ruleset) that should not apply for the yield study. In particular, if you do not want any of the reservoirs in the subbasin to divert water, disable the Compute Reservoir Diversions rule. If you want all non-yield reservoirs to divert as defined, then you will need to modify the standard ruleset. First, create an identical subbasin to the one specified in the Compute Reservoir Diversions rule. Then remove the reservoir, diversion and water user objects for which you are finding the yield. Use this new subbasin in the Compute Reservoir Diversion rule. This way, you will compute reservoir diversions for all reservoirs except those for which you are finding the yield. Other rules may or may not need to be disabled depending on the desired policies in place during the yield study.
4. Import the yield study iterative MRM ruleset YieldStudy.rls.gz.
a. Open the MRM policy set by selecting the workspace menu item Policy, then Iterative MRM Rules Set.
b. This will open the Iterative MRM Rules. To initiate the import into this set, select File, then Import Set. Select the file YieldStudy.rls.gz.
c. This will open the import dialog which will display the policy group and utility group contained in the file; confirm that the items being imported do not conflict with existing names in your MRM policy and continue with the import.
d. Set the Agenda Order of the MRM ruleset to “1,2,3,..”. This is done from the MRM Rules - Ruleset Editor View, then Show Advanced Properties menu. The Agenda Order is controlled by two toggles added to the bottom of the dialog.
e. Specify which algorithm you wish to use. Turn on only one of either Rule 1, 2, or 3. Rule 1 specifies a bisection algorithm to find the solution. Rule 2 employs a combination bisection/heuristic search algorithm (Heuristic A) which uses the bisection method when the yield is too high and a heuristic approach when the yield is too low. In this latter case, it estimates the additional yield necessary to lower the reservoir to the conservation pool during the critical period. Rule 3 triggers a faster heuristic algorithm (Heuristic B) which tries the intermediate yield first and then uses the calculation after each successful fun. See “Algorithms” for details on these algorithms.
f. Specify whether you want to use the average Yield or Distribute the Yield by enabling or disabling MRM rules 4 or 5. Rule 4 triggers a yearly distribution of yield. Rule 5 uses a constant yield.
g. The RPL set should now look similar to Figure 5.2 with your combination of enabled and disabled rules. No other rules in the set need to be disabled.
Figure 5.2 Yield study iterative MRM RPL set
h. Figure 5.3 and Figure 5.4 show two additional changes you may need to make to the functions, depending on how the reservoirs are modeling inflows and evaporation.
Note: If you are using Heuristic A or Heuristic B, you may need to change the function EvaporationFromStorage to access the correct Evaporation Rate slot. It should reference the slot with input data.
Figure 5.3
Note: If you are computing the maximum yield, you may need to change the function Average Natural Flow to access the correct hydrologic inflow slots. It should reference the slot with input data.
Figure 5.4
5. Create an MRM configuration for the yield study. See “Iterative Runs” in Solution Approaches for details on iterative MRM.
a. Open the Multiple Run Control Dialog by selecting the appropriate workspace menu button or selecting Control, then MRM Control Panel.
b. Create a new configuration MRM control dialog by selecting Configuration, then New.
c. To edit the new configuration, double-click its name in the MRM Run Control Dialog.
d. This will open the MRM Configuration Dialog. Select Iterative mode and then select the Iterative Runs tab.
e. In this tab, use the Add button to add the first seven (1–7) rules to the upper Pre-Run Rules box.
f. Use the second Add button to add the remaining rules, 8–20, to the Post-Run Rules box.
g. Select Continue After Abort and set Max Iterations to a number which is appropriate.
h. Select that the Pre-Run Rules should execute Before First Run. Your screen should look similar to Figure 5.5.
i. Select OK to apply the changes and close the window.
Figure 5.5 Iterative MRM configuration
6. At any time before, during or after the run, you can open an SCT to see all the results of the run to that point. The SCT file is in YieldStudy.sct. If doing a multiple reservoir yield study, insert additional columns to show each column of the Yield Agg series slot. The column labels of the SCT can be renamed using the Slots, then Set Label/Function menu. Make sure the SCT is unlocked or this option will not be available.
7. Conduct the MRM run as follows: In the Multiple Run Control, select the new MRM configuration on the Multiple Run Control dialog and select the Run button.
8. After the run, the sequence of values tried for the individual reservoir yields may be found in the Yield slot of the Yield Study Data object. The easiest way to view all results is through the YieldStudy.sct.
Viewing Results
Figure 5.6 shows sample results. The Bisection method converged in 35 iterations. This section provides some guidance on viewing the SCT.
The SCT can be read as follows: Each row represents an iterative run. The average yield used for each run can be found in the Yield.Res column. For example, in the first run the minimum yield of 20 cfs was used for Dequeen, 10cfs for Dierks and 50 cfs for Millwood. In the next row, the maximum for Dequeen is used while the other two reservoirs continue to use the previous value. Then the yield for Dequeen is bisected. Only Dequeen’s Yield is modified until it converges, then the algorithm moves on to Dierks. The Minimum Level Difference column shows the minimum difference between pool elevation and the bottom of the conservation pool.
Note: Convergence is met in rows 13, 24, and 35 where this value is less than 0.1ft.
Note: The yields are average values, while the distributed values are set on the Reservoir.Diversion slot and can be viewed there. To determine the total yield, highlight each of the individual yields as shown and the sum is displayed at the bottom of the SCT. The SCT also contains (not shown) the bounds used in iteration and the critical period found for each run. At the end of the iterative run, the critical period can be found on the row in which that reservoir converged, i.e. 13, 24, and 35.
Figure 5.6 SCT used to view results from Yield study
Algorithms
Following is a description of the available algorithms.
Bisection
The Bisection algorithm is the most basic and most robust algorithm implemented. All other algorithms fall back to the bisection if the individual run does not succeed. In Bisection, the minimum and maximum yield is tried first. Then the min and max are averaged or bisected to find the intermediate yield and a run is made with that value. After the third run, the algorithm decides if the yield is too high or too low and modifies the upper or lower bound as appropriates and bisects again. This procedure continues until the solution is found. It is robust as the min and max yields are tried first to bound the solution. No additional information on the reservoirs or physical processes are used, so it is often the simplest to get working. It can be slow as it uses a brute force approach; no information on the processes are used to estimate the next yield to try.
Heuristic A
In Heuristic A, first the minimum, then the maximum yields are tried. Then the average of those two yields is tried. If this third and subsequent yield estimate is too high, meaning the minimum level difference is negative, the bisection method will be used as described above. If the minimum level difference is positive the following approach will be taken to compute the next yield.
Assume that we have completed a simulation with a yield which resulted in a positive minimum level difference, i.e. the reservoir is above the bottom of conservation pool throughout the run. In this case, we have underestimated the yield. Examining the results from the simulation, we can find the dates of the drawdown period defined as the last date when the reservoir was full (at the top of the conservation pool) to the date of the minimum level difference. If we had guessed the correct yield then the drawdown period would have ended in a minimum level difference of zero, but we know that we underestimated the diversion because there is water remaining in the conservation pool at the end of the drawdown period. To exactly drain the conservation pool during the drawdown period, we would have needed to divert additional storage equal to the volume of the conservation pool at the minimum level difference date as well as enough to compensate for the reduced evaporation which would result from lower elevations over the drawdown period.
Figure 5.7 shows a plot of storage versus time for this situation. In this figure, the curve Sr is the storage produced from the previous run. Additional water must be released to lower the pool to the bottom of conservation pool. The shaded area is the volume of water that must be released to scale the solid black curve to reach the bottom of conservation pool. This would produce a curve similar to the dotted blue curve.
Figure 5.7 Plot of a sample drawdown period
This analysis motivates Equation 5.1 for using the results from one run to choose a yield which will lead to a minimum level difference of zero in the next run.
(5.1)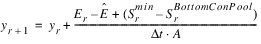 
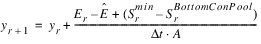
where:
– y = average yield
– r = run number, r is the previous run, r+1 is the next run
– Smin = minimum storage that occurred (i.e., storage at minimum level difference date)
– SBottomConPool = storage corresponding to an empty conservation pool
– A = average yield distribution factor over the drawdown period. The yield may be distributed to the Reservoir Diversion based on factors representing the percentage/fraction of the average yield. These factors are stored in the Distribution Yield periodic slot and must average to 1.0 over the course of a year. Otherwise an error is issued and the run stops. Because of this distribution, the average of the yield over the critical period may not be 1.0. In this equation, we divide by the average distribution factor over this period to ensure that we are still dealing with average yield.
– 
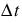= Duration of the drawdown period, tbegin to tend
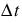= Duration of the drawdown period, tbegin to tend – E = Total evaporation over drawdown period
– Ê = Estimated total evaporation that would occur over the drawdown period if the true yield were released. Increasing the yield from the last run will lead to lower storage values over the drawdown period, which will in turn lead to a lower evaporation over the drawdown period. We estimate Ê by computing the evaporation which would result from a drawdown period whose Storage (S) is like the previous run’s Storage, except it is scaled so it reaches the bottom of the conservation pool at the end of the drawdown period (i.e., the blue dotted line in the figure). The estimate for the storage during the drawdown period when we are using the true yield is calculated using Equation 5.2.
(5.2)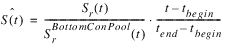 
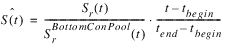
where:
– tbegin = the begin date of the drawdown period
– tend = the end date of the drawdown period
Then we can use this along with the method for computing evaporation as a function of storage, Evap(S(t)), to compute the total estimated evaporation over the drawdown period using Equation 5.3.
(5.3)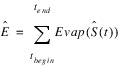 
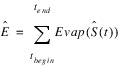
Heuristic B
In Heuristic B, the minimum and maximum yields are computed to bound the solution, but no runs are made with the values. Instead the average of them is used on the first run (If the Reservoir Data for Bisection.Initial Yield to Try is not specified). Then after each successful run, regardless of whether the minimum level difference is positive or negative, the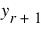 
is computed using Equation 5.1 and used on the next run. On unsuccessful runs, a bisection is used.
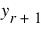is computed using Equation 5.1 and used on the next run. On unsuccessful runs, a bisection is used. Choosing a Method
Table 5.1 summarizes the strengths and weaknesses of each algorithm. This is particularly important for long model runs where any extra runs means hours of computations. own.
Algorithm | Strengths | Potential Weakness |
|---|---|---|
Bisection | Most robust and easy to understand. Requires the least amount of effort if evaporation or other physical processes are involved. | Potentially slow as runs are made to ensure the upper and lower bounds encompass the solution point. Also slower as it just keeps going until a solution is found. No information from the run is used to guide the next run. |
Heuristic A | Potentially faster than bisection. Like Heuristic B, information from this run can be used to guide the trial in the next run. | Because the heuristic is only used for positive minimum elevation differences, the search may be close to the final solution but then has a negative minimum elevation, so then uses bisection and jumps away from the final solution. |
Heuristic B | Faster; the first two runs for each reservoir are skipped and the estimated yield is always used for the next run. | Because the upper and lower bounds are not tried first, the solution could be outside the bounds and would not be caught until hitting max iterations and/or attempting to converge on the bound. |
Revised: 11/11/2019